Maturatraining Mathematik
Matura-Vorbereitung für alle Schultypen
Alles, was du für dein Maturatraining Mathematik brauchst!
Mit eSquirrel können alle Grundkompetenzen für die Matura Mathematik (SRDP) geübt werden. Mit passenden Frageformaten werden SchülerInnen bestens direkt am Smartphone vorbereitet. Jede einzelne Frage ist zusätzlich mit einem Erklärvideo von Mathago ausgestattet.






Für Mathe-LehrerInnen: Unterstützung für die Matura Mathematik-Vorbereitung
Mit einer kostengünstigen Klassenlizenz von eSquirrel können Sie Ihre SchülerInnen ideal in der Vorbereitung für die Zentralmatura unterstützen. Bereits ab 3 SchülerInnen bestellbar und somit die ideal für die individuelle Förderung. Alle Kurse können über Unterrichtsmittel eigener Wahl (UeW) bestellt werden.




Bei Fragen kontaktieren Sie uns gerne unter [email protected] per Mail oder telefonisch unter +43 1 330 5453.

Wir garantieren: mit uns schaffst du die Mathematik-Matura!
Das bestätigen zahlreiche Lerninstitute und LehrerInnen!
Mit den Erklärvideos von Mathago findest du Antworten auf all deine Fragen.
So erhältst du dein Matura-Training in der eSquirrel-App!

Schritt 1
eSquirrel downloaden
Die Lern-App „eSquirrel“ im App-Store (iOS) oder Google Play-Store (Android) downloaden und installieren.

Schritt 2
Account anlegen
Leg dir ganz einfach einen Account an

Schritt 3
QR-Code scannen
oder “Maturatraining” im Store der eSquirrel-App suchen


Schritt 4
Lerne effizient
und unterhaltsam
Entdecke das volle eSquirrel-Erlebnis und schaffe die Matura garantiert!
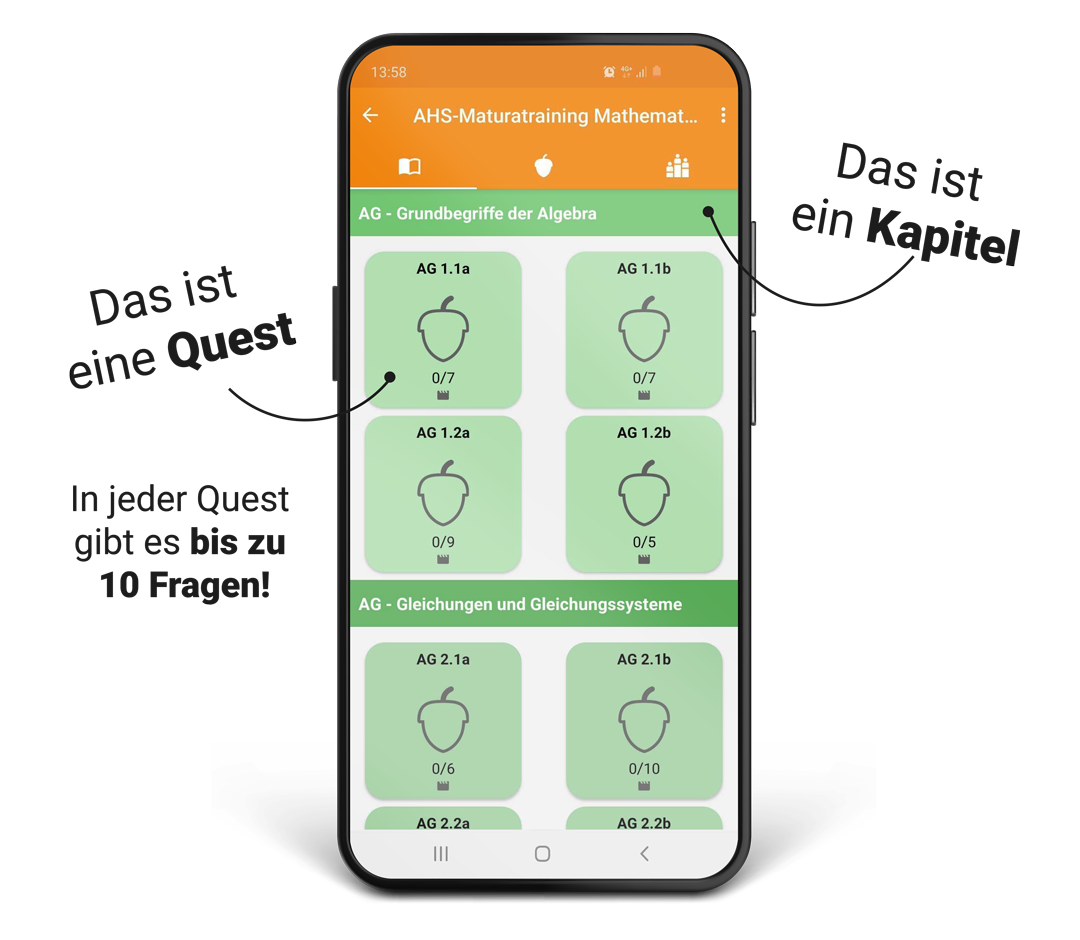
Maturavorbereitung für die Mathematik Zentralmatura mit Kursen von eSquirrel
Bei der Maturavorbereitung für die Mathematik-Zentralmatura mit Kursen von eSquirrel können alle 73 Grundkompetenzen geübt werden – durch Wiederholen am Handy werden alle Inhalte im Langzeitgedächtnis gespeichert. Bessere Noten inklusive!
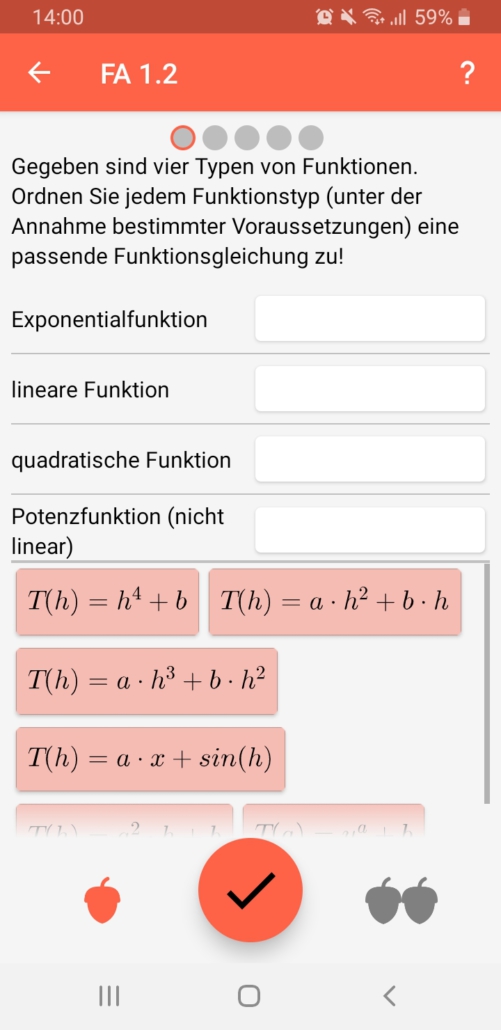
Die eSquirrel-Kurse „Maturatraining Mathematik“ dienen zur Vorbereitung auf die Mathematik-Zentralmatura aller Schultypen. Die Vorbereitungskurse auf der Zentralmatura basieren auf den 73 Grundkompetenzen und setzen sich zusammen aus Algebra und Geometrie, Analysis, Funktionale Abhängigkeiten sowie Wahrscheinlichkeit und Statistik.


Was AbsolventInnen zum Maturatraining sagen:
Mit eSquirrel konnte ich mich effizient auf die Mathematura vorbereiten. So macht das Lernen sogar Spaß, gerade wenn man im Leaderboard vorne sein möchte!
– Lisa-Marie U. Maturantin am Sacré Coeur Wien
„Mein Lehrer hat mir voriges Jahr gesagt, wenn du alles aus der App eSquirrel kannst, bestehst du die Matura. Und so war es auch!“
– Lisa, 20 Studentin, hat 2021 die Matura bestanden
„Die intuitive Bedienung und die Erklärvideos, es haben sich bei mir Fragen beantwortet, die ich so nicht verstanden hätte.“
„Ich finde es gut, dass auf man mit der App wirklich überall und rund um die Uhr lernen kann- egal wo, ob in der Straßenbahn oder zu Hause.“


Fragen & Antworten
Maturatraining Mathematik
Für wen ist das eSquirrel-Maturatraining geeignet?
Das eSquirrel-Maturatraining richtet sich an alle LehrerInnen, die ihre SchülerInnen optimal, nachhaltig und stressfrei auf die Mathematikmatura vorbereiten wollen. Für jeden Schultyp in Österreich gibt es dazu ein eigenes Angebot: AHS, HTL, HAK, HUM/HLFS und Berufsreifeprüfung! Außerdem ist es für MaturantInnen geeignet, die Mathematik verstehen und die Maturaprüfung bestehen möchten, ohne dabei langweilige Bücher herumschleppen zu müssen.
Gibt es eSquirrel-Kurse auch zu Mathematik-Schulbüchern der Sekundarstufe 2?
Ja! Zu den AHS-Reihen Lösungswege und Mathematik verstehen (öbv) gibt es eSquirrel-Kurse, die genauso wie das Maturatraining von der 5. bis zur 8. Klasse AHS als Begleitung im Unterricht und Vorbereitung auf die Matura verwendet werden können. Außerdem gibt es noch DAS Mathematikbuch – Willkommen in der Oberstufe fürs Gymnasium, sowie Genial! Mathematik PTS und DAS Mathematikbuch für die PTS für die Polytechnische Schule (“Poly”) vom Bildungsverlag Lemberger.
Kann ich den Kurs als LehrerIn testen?
Ja! Legen Sie sich in unserem LehrerInnen-Portal kostenlos einen Account an und klicken Sie “Neue Klasse”. Suchen Sie sich Ihren passenden Maturakurs aus und wählen Sie die Option “1 Monat gratis testen”. Kleiner Tipp: Sie können alle eSquirrel-Kurse 1 Monat lang gratis testen, ohne automatische Verlängerung.
Wie erhalte ich die Vollversion als LehrerIn?
- Gehen Sie in unseren Shop und suchen Sie sich einen oder auch mehrere passende Kurse aus.
- Legen Sie diese in den Warenkorb und gehen weiter zur Bezahlung.
- Alle Produkte können auch mit UeW bestellt werden. Wählen Sie bei den Rechnungsinformationen die Option “Als Unterrichtsmittel eigener Wahl (UeW) bestellen (AT)” und geben Ihre Schulkennzahl an.
Klassenlizenzen sind ab 3 SchülerInnen bestellbar und somit auch ideal zur individuellen Förderung geeignet.
Kann ich den Kurs als SchülerIn testen?
Für jeden eSquirrel-Kurs gibt es auch eine Demoversion. Dabei kannst du bereits 15 % des Inhalts kostenfrei testen. Lade dazu dir die eSquirrel-App. Suche zunächst deinen gewünschten Kurs aus und klicke auf „Demo“. Du kannst danach jederzeit auf die Vollversion umsteigen.
Wie erhalte ich die Vollversion als SchülerIn?
Die Einzellizenz kannst du in am bequemsten im Store in der eSquirrel-App kaufen. Suche dazu zunächst deinen gewünschten Kurs aus und klicke auf „Kaufen“. Danach kannst du die Zahlungsmethode wählen, die du mit deinem Google- oder Apple-Konto verknüpft hast. Nach der Zahlung steht dir der Inhalt des Kurses in deinem Konto sofort zur Verfügung. Kein Warenkorb, kein Versand, keine Lieferung.
Für alle weiteren Fragen besuche unsere FAQs.